Answer to Describe the level curves of the function z = x2 Math;By default this expression is x^2 y^2 So if x = 2, and y = 2, z will equal 4 4 = 0 Try hovering over the point (2,2) above You should see in the sidebar that the (x,y,z) indicator displays (2,2,0) So, that explains why we see a contour line along the lineLevel curves of a function calculator Level curves of a function calculator M1c Exam1 Notes F14 Level curves of a function calculator Level curves of a function calculatorCasio Graphics Calculator Fx 9750gii Amazon Co Uk Normal Distribution Calculator High Accuracy Calculation
1
Level curves of a function calculator
Level curves of a function calculator-Add a Calculator application to a TINspire document and enter the following Solving z = f(x;y) succeeded and there are two solutions which can be used to create lists of functions to plot the level curves Step 2 Graph z = f(x;y) and use the menu item Trace zTrace to determine theDescribe the level curves of the function and sketch the levelcurves for the given c values f(x,y) = x2 2y2, c = 0, 2, 4, 6, 8 Get more help from Chegg Solve it with our calculus problem solver and calculator




Fx 991ex Classwiz Non Programmable Scientific Calculator Casio
With this ability, you could flow across continuouslyspaced level curvesExample 1 Let f ( x, y) = x 2 − y 2 We will study the level curves c = x 2 − y 2 First, look at the case c = 0 The level curve equation x 2 − y 2 = 0 factors to ( x − y) ( x y) = 0 This equation is satisfied if either y = x or y = − x Both these are equations for lines, so the level curve for c = 0 is two lines If youGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!
Double checking my own approximation to the function for a solution to the inf circular potential well in QM 4 1426 years old level / Highschool/ University/ Grad student / Useful /The calculator will find the tangent line to the explicit, polar, parametric and implicit curve at the given point, with steps shown It can handle horizontal and vertical tangent lines as well The tangent line is perpendicular to the normal lineMathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields It only takes a minute to sign up
The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any number So the equations of the level curves are \(f\left( {x,y} \right) = k\) Note that sometimes the equation will be in the form \(f\left( {x,y,z} \right) = 0\) and in these cases the equations of the level curves are \(f\left( {x,y,k} \right) = 0\) A level curve of a function f(x,y) is a set of points (x,y) in the plane such that f(x,y)=c for a fixed value c Example 5 The level curves of f(x,y) = x 2 y 2 are curves of the form x 2 y 2 =c for different choices of c These are circles ofDescribe the level curves of the function z = x2 5y2




Fx 991ex Classwiz Non Programmable Scientific Calculator Casio
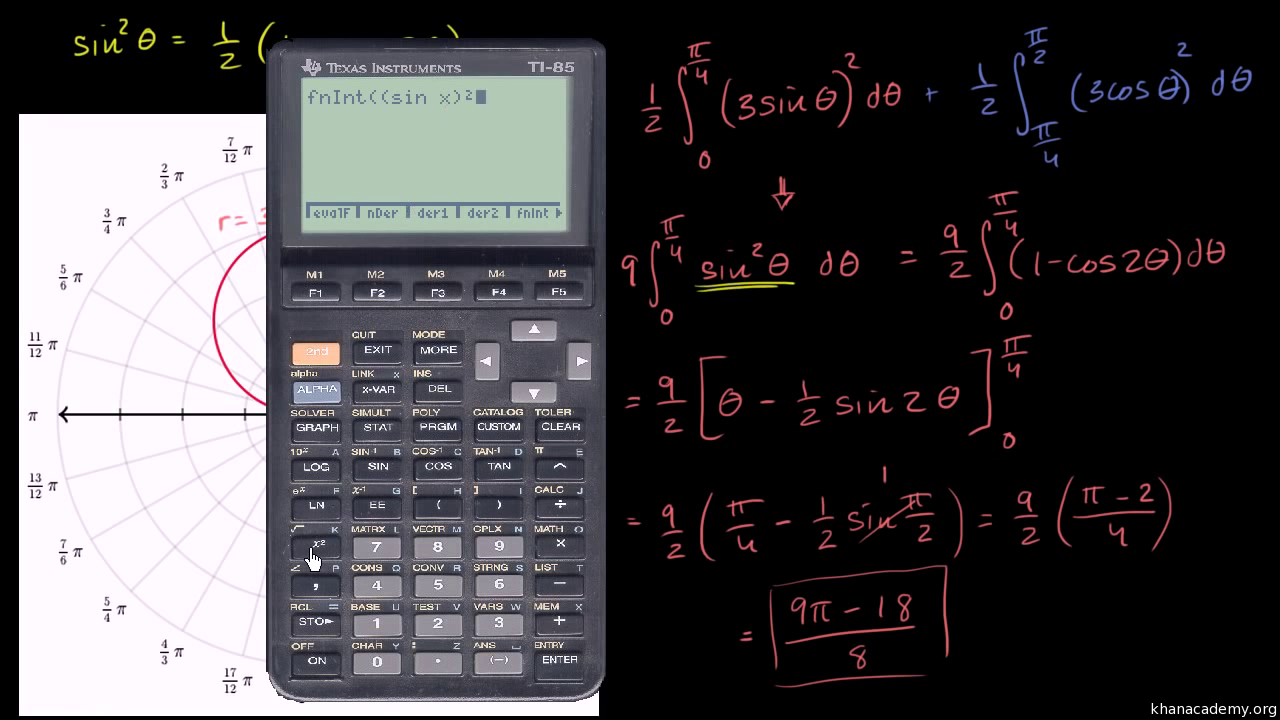



Parametric Equations Polar Coordinates And Vector Valued Functions Khan Academy
Level curves The two main ways to visualize functions of two variables is via graphs and level curves Both were introduced in an earlier learning module Level curves for a function z = f ( x, y) D ⊆ R 2 → R the level curve of value c is the curve C in D ⊆ R 2 on which f C = c Notice the critical difference between a level curve CFree ebook http//tinyurlcom/EngMathYT How to sketch level curves and their relationship with surfaces Such ideas are seen in university mathematics andLevel surfaces For a function $w=f(x,\,y,\,z) \, U \,\subseteq\, {\mathbb R}^3 \to {\mathbb R}$ the level surface of value $c$ is the surface $S$ in $U \subseteq




Level Curves Of Functions Of Two Variables Youtube




Math 148 Exam Iii Practice Problems
Functions & Graphing Calculator \square!Level Curves Def If f is a function of two variables with domain D, then the graph of f is {(x,y,z) ∈ R3 z = f(x,y) } for (x,y) ∈ D Def The level curves of a function f(x,y)are the curves in the plane with equations f(x,y)= kwhere is a constant in the range of f The contour curves are the corresponding curves on the surface, theCurve sketching is a calculation to find all the characteristic points of a function, eg roots, yaxisintercept, maximum and minimum turning points, inflection points How to get those points?




Level Curves Curves Level Stvincent Glogster Edu Interactive Multimedia Posters
:max_bytes(150000):strip_icc()/3669694_sd-5b9fc7d9c9e77c0050e5b11d.jpg)



The 9 Best Graphing Calculators Of 21
Plug the coordinates of the point in your function to get $f(x,y)=6$ Thus the level curve is $$16x^2y^2=6$$ Or $$x^2y^2=10$$ which is a circle centered at the origin with radius $R=\sqrt {10}$ Share I am being asked to calculate level curves for the following equation f(x,y)=e^(2x^22y^2) but I do not know where to start Any adviceLevel Curve Grapher Level Curve Grapher Enter a function f (x,y) Enter a value of c Enter a value of c Enter a value of c Enter a value of c



Online Area Calculator Between Two Crossed Curves




Draw A Contour Map Of The Function Showing Several Chegg Com
Share a link to this widget More Embed this widget » Added by RicardoHdez in Mathematics The level curves of f (x,y) are curves in the xyplane along which f has a constant value Send feedback Visit WolframAlphaVideo Transcript {'transcript' "problem were sketching the level curve for the function F X Y is equal to X squared plus y squared for the given values have seen I've done so using decimals, the online calculator analogy to enter the equations that it did go to see entered the given values of C, and this would be the resulting graph"} Level curves Author Siamak The level curves of two functions and Blue represents and red represents Since and are both harmonic and is a harmonic conjugate of , the level curves of and intersect each other at right angles
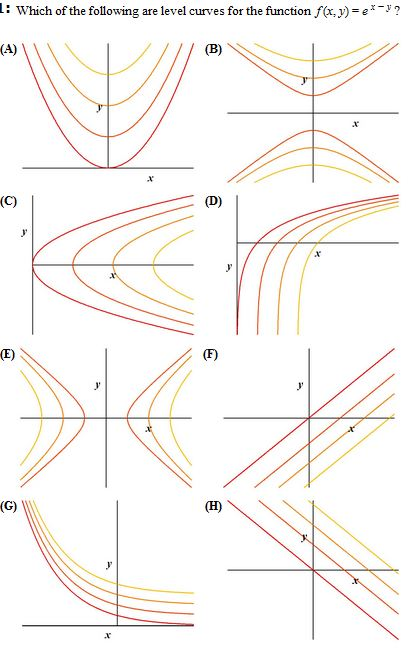



Which Of The Following Are Level Curves For The Chegg Com




The 9 Best Graphing Calculators Of 21
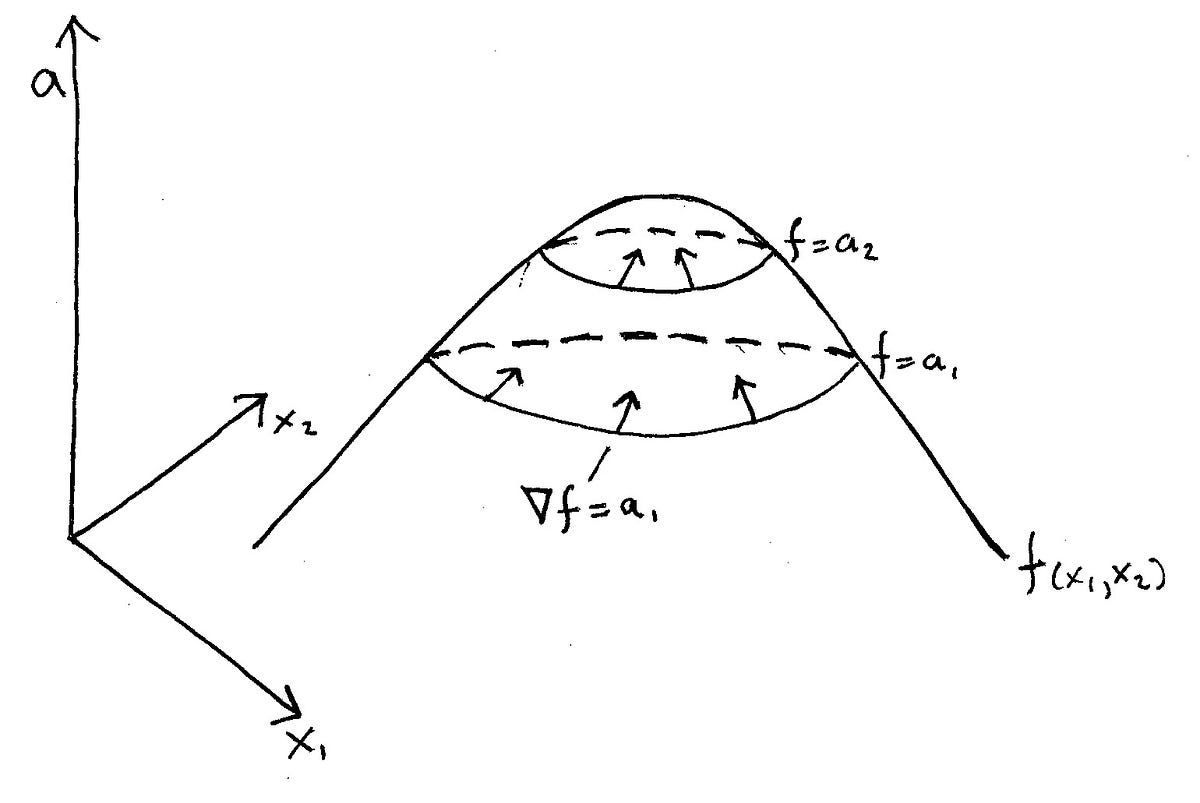
Of the boot They correspond to the bottom four level curves in Figure 11 Estimating function values from level curves Level curves of a function, as in Figure 13, show where the function has each of the zvalues for the given curves, and we can estimate the function's values at other points from values on nearby level curves, 40 60 80 −3 These level curves and gradient vector fields are slowly building an outline of a surface in \( \mathbb{R}^3\) However, we are still lacking a way of connecting the curves and the arrows How would one follow the vectors to get from one level curve to the next?A level curve of a function of two variables is completely analogous to a contour line on a topographical map (a) A topographical map of Devil's Tower, Wyoming Lines that are close together indicate very steep terrain (b) A perspective photo of Devil's Tower shows just how steep its sides are Notice the top of the tower has the same




Best Graphing Calculators In Depth Buyer S Guide
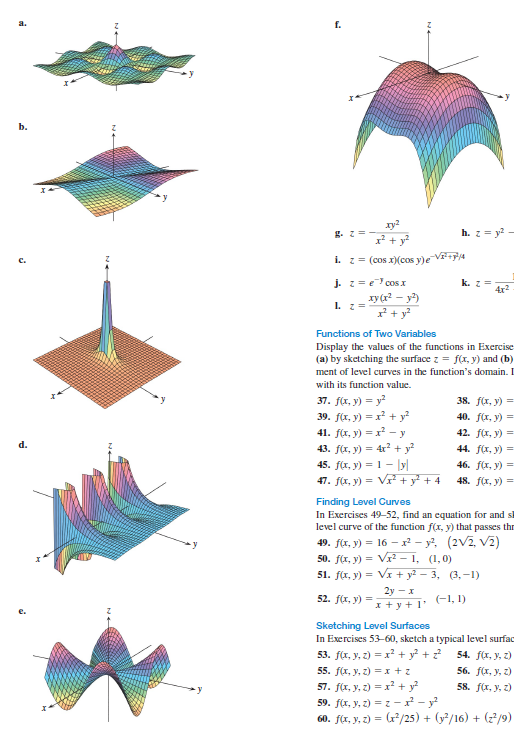



Matching Surfaces With Level Curves Exercises 31 36 Chegg Com
Level Curves The level curves f (x, y) = k are just the traces of the graph of f in the horizontal plane z = k projected down to the xyplane So if you draw the level curves of a function and visualize them being lifted up to the surface at the indicated height, then you can mentally piece together a picture of the graph In the section we introduce the concept of directional derivatives With directional derivatives we can now ask how a function is changing if we allow all the independent variables to change rather than holding all but one constant as we had to do with partial derivatives In addition, we will define the gradient vector to help with some of the notation and work here Level curve calculator in Description DgFlick Edit Xpress STD DgFlick Edit Xpress is an easy to use photo correction tool You get basic editing tools like BCG, RGB, Level, Curve and advanced editing tools like Lasso, Chroma, Touchup, Highlighter, etc Batch editing feature lets you color correct 1000s of the photos in a single click
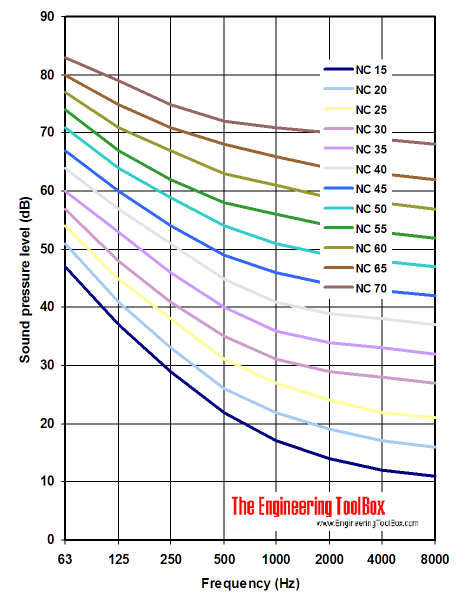



Nc Noise Criterion



A Simple Explanation Of Why Lagrange Multipliers Works By Andrew Chamberlain Ph D Medium
If the calculator did not compute something or you have identified an error, or you have a suggestion/feedback, please write it in the comments below Your input find the area between the following curves $$$ y = x^{2} $$$ , $$$ y = \sqrt{x} $$$ on the interval $$$ \left(\infty, \infty\right) $$$Calculus questions and answers;A level curve can be drawn for function of two variable ,for function of three variable we have level surface A level curve of a function is curve of points where function have constant values,level curve is simply a cross section of graph of f



Level Sets Ximera




Gradients And Level Curves
Note how the \(y\)axis is pointing away from the viewer to more closely resemble the orientation of the level curves in (a) Figure \(\PageIndex{5}\) Graphing the level curves in Example 1214 Seeing the level curves helps us understand the graph For instance, the graph does not make it clear that one can "walk'' along the line \(y=xReturning to the function g (x, y) = 9 − x 2 − y 2, g (x, y) = 9 − x 2 − y 2, we can determine the level curves of this function The range of g g is the closed interval 0, 3 0, 3 First, we choose any number in this closed interval—say, c = 2 c = 2 The level curve corresponding to c = 2 c = 2 is described by the equationOkay, we're on number thirty six in section four point four We have the function f vexes You could eat it, X, and we have a value for X, and we're just asked




Calculus Iii Functions Of Several Variables
/ScreenShot2020-02-11at12.52.56PM-a9175650691c48c18cdff16e42fdb830.png)



The 9 Best Graphing Calculators Of 21
1 Level Surfaces 2 If one of the Arguments is time we can animate ie w = f(x,y,t) Level Surfaces Given w = f(x,y,z) then a level surface is obtained by considering w = c = f(x,y,z) The interpretation being that on a level surface f has the same value at every pt For example f could represent the temperature at each pt in 3spaceThe procedure to use the area between the two curves calculator is as follows Step 1 Enter the smaller function, larger function and the limit values in the given input fields Step 2 Now click the button "Calculate Area" to get the output Step 3 Finally, the area between the two curves will be displayed in the new windowBy calculating derivatives Then you set the function as well as the derivative equal to zero Roots are solutions of the equation




Amazon Com Casio Prizm Fx Cg50 Color Graphing Calculator Everything Else




How Do You Sketch Level Curves Of Multivariable Functions Vector Calculus 2 Youtube
How to Find the Level Curves of a Function Calculus 3 How to Find the Level Curves of a Function Calculus 3 Homework Statement I have this function of two variables f(x,y)=x^24xy^2 Where I have to compute the level curves for f(x,y)=3, 2, 1, 0, 1 Homework Equations The Attempt at a Solution So yeah well I know that I have to draw the following curvesCalculates a table of the probability density function, or lower or upper cumulative distribution function of the beta distribution, and draws the chart




Best Graphing Calculators In Depth Buyer S Guide



1
The function z = ¨ xy ¨ In17= Plot3D@Abs@xyD, 8x,1, 1 30, Mesh> False, AxesLabel> 8"x","y","z"A level curve of a function $f(x,y)$ is the curve of points $(x,y)$ where $f(x,y)$ is some constant value A level curve is simply a cross section of the graphLevel Curves (ie Contours) and Level Surfaces Consider a function For any constant we can consider the collection of points satisfying the equation This collection of points is generally called a level surfaceWhen we generically have a (true 2dimensional) surface For example The level surface of at level is the unit sphere (the sphere of radius 1 centered at the origin)




Level Curves




Solved Lim X Y 1 2 3 Prove 2 Using The Epsilon Delta Chegg Com
Free functions calculator explore function domain, range, intercepts, extreme points and asymptotes stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyLevel Curves Author Kristen Beck Topic Functions This worksheet illustrates the level curves of a function of two variables You may enter any function which is a polynomial in both andDefinition The level curves of a function f of two variables are the curves with equations f (x,y) = k, where k is a constant (in the range of f ) A level curve f (x,y) = k is the set of all points in the domain of f at which f takes on a given value k In other words, it shows where the graph of f



Desmos Accessibility



Level Sets Ximera
Select a function from the dropdown menu or type your own function in the text box below and click "Enter" to plot it Click the radio buttons to view either a level curve or a cross section Use the slider to change the value of the related constant k, c, or d Click "Reset" to reset both plots




The Graphs Below Show The Level Curves For A Function Chegg Com
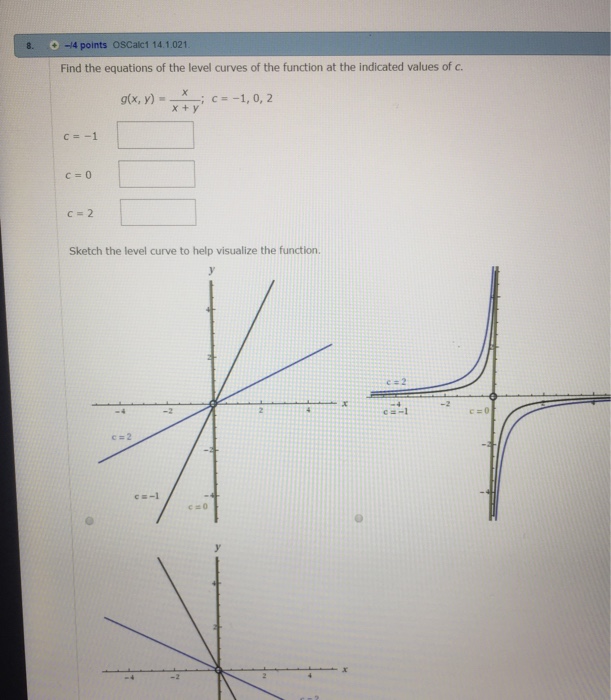



Find The Equations Of The Level Curves Of The Chegg Com




How Do You Sketch Level Curves Of Multivariable Functions Krista King Math Online Math Tutor



Relief Functions And Level Curves




Finding A Function With Level Curves Mathematics Stack Exchange




Level Curves Mit 18 02sc Multivariable Calculus Fall 10 Youtube



Area Between Two Curves Calculator Find Area Between Curves
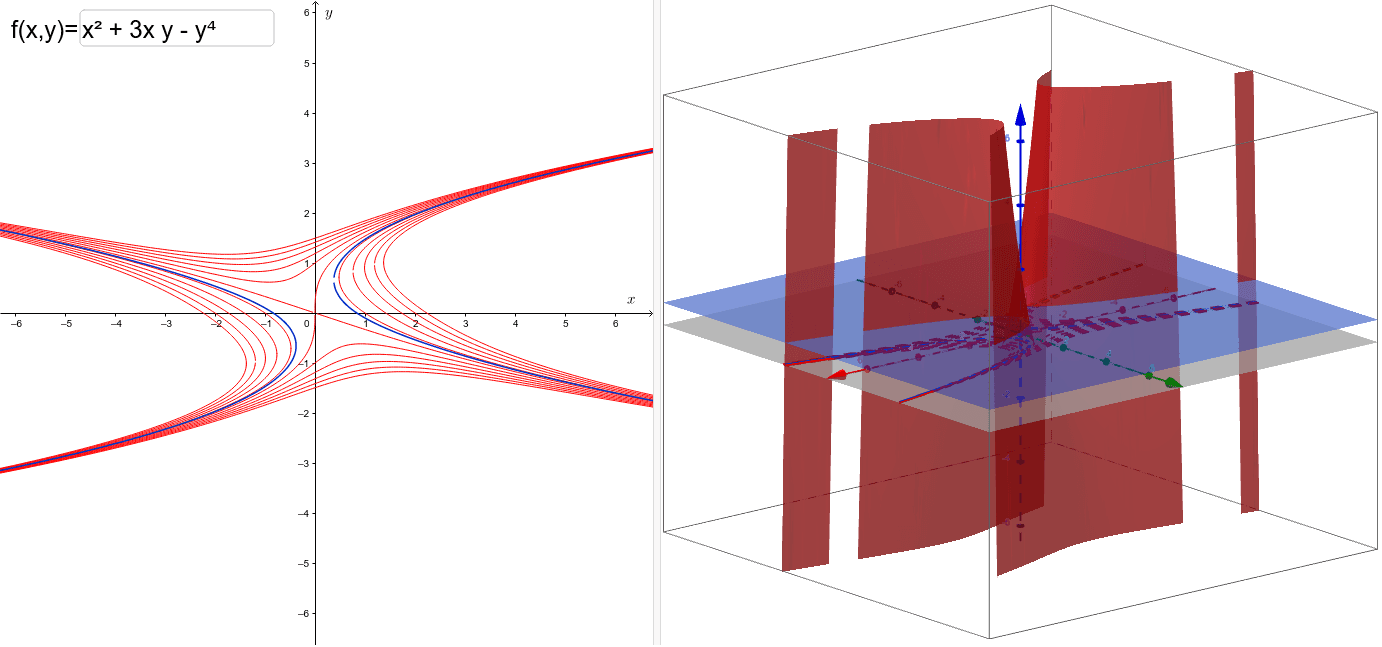



Level Curves Geogebra




Fx 991ex Classwiz Non Programmable Scientific Calculator Casio



Directional Derivative




Desmos Review For Teachers Common Sense Education



Level Sets Ximera




Sketch The Level Curves Of The Function G X Y Chegg Com



1




Top 7 Uses For A Graphing Calculator Hp Tech Takes




Level Sets Math Insight



Level Curves




How To Sketch Level Curves Vector Calculus Youtube
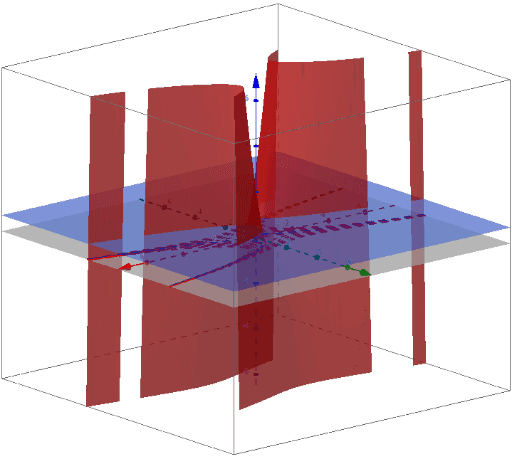



Level Curves Geogebra




Calculus Iii Functions Of Several Variables




Approximating Limits On A Graphing Calculator Video Lesson Transcript Study Com




How Do You Sketch Level Curves Of Multivariable Functions Vector Calculus 3 Youtube




14 1 Functions Of Several Variables Mathematics Libretexts




Level Sets Math Insight
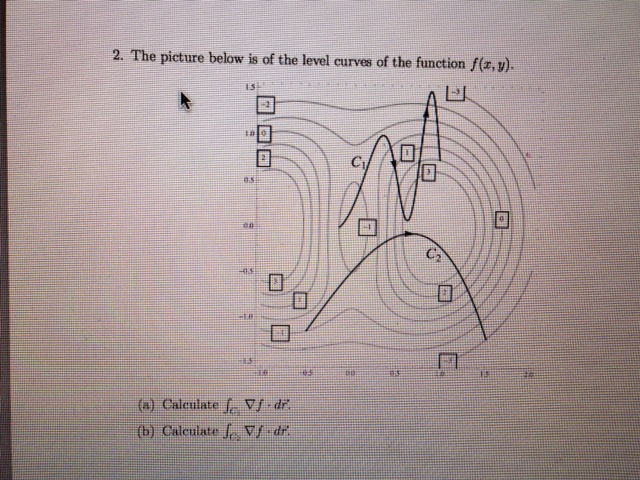



The Picture Below Is Of The Level Curves Of The Chegg Com




Level Set Examples Math Insight



Experience Bulbapedia The Community Driven Pokemon Encyclopedia
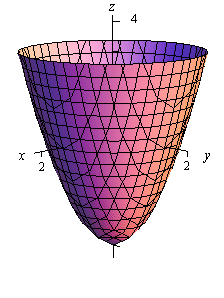



Calculus Iii Functions Of Several Variables




Level Surfaces




Calculus Iii Functions Of Several Variables




Cal123 Level Curves And Contour Diagrams Pdf Contour Line Curve
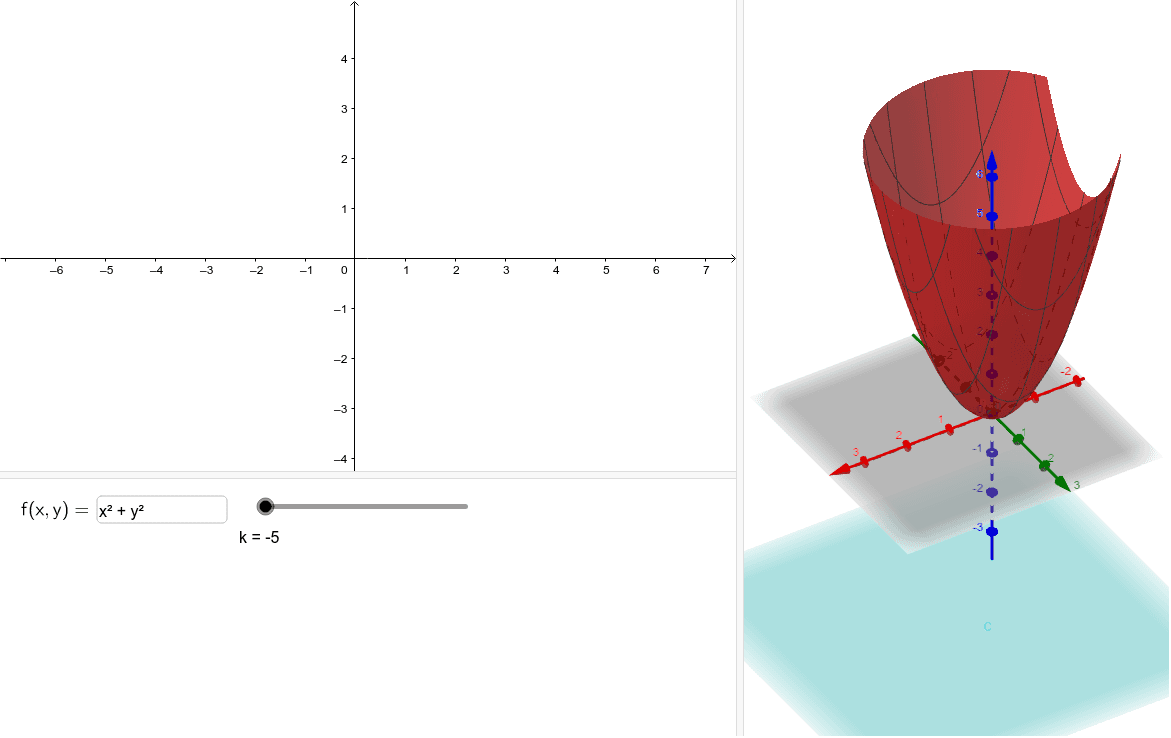



Level Curves Geogebra



Desmos Graphing Calculator Enhances Your Math Instruction New Jersey Education Association




Calculus Iii Functions Of Several Variables



Clim 301 Hw 1




Calculation Of The Minimum Ecological Water Level For The Honghe Download Scientific Diagram




Level Sets Math Insight




How To Sketch Level Curves Youtube




Normal Distribution Calculator High Accuracy Calculation




A Illustrates The Results Of Calculation Of The Additional Displacement Download Scientific Diagram




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware




How To Find The Level Curves Of A Function Calculus 3 Youtube
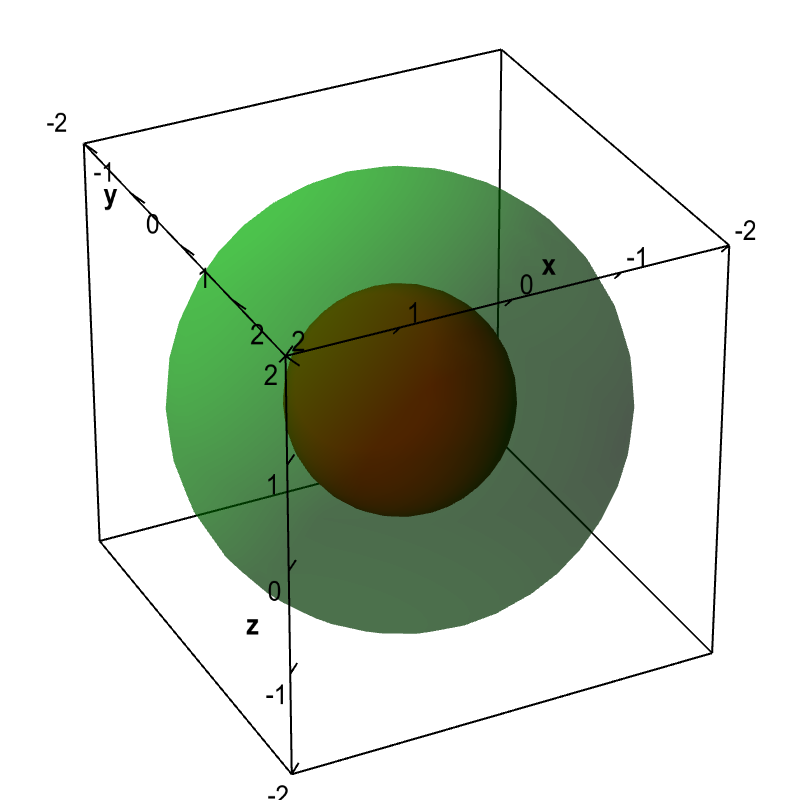



Level Set Examples Math Insight
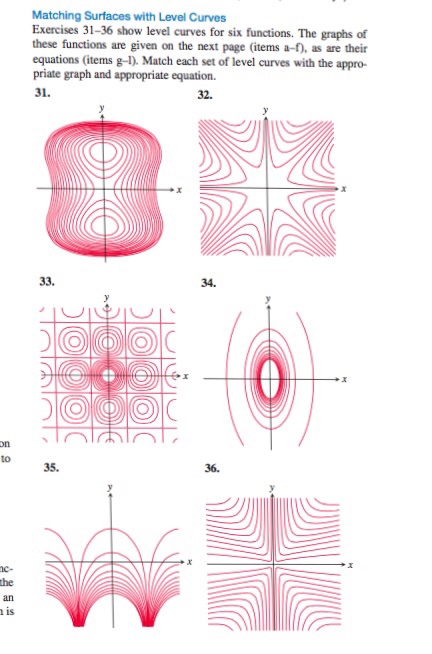



Matching Surfaces With Level Curves Exercises 31 36 Chegg Com




Level Set Wikipedia



Straight Level And The Curvature Of The Earth Math Encounters Blog



Inverse Square Law




Level Set Wikipedia



The Gradient And Directional Derivative




Saddle Point Wikipedia
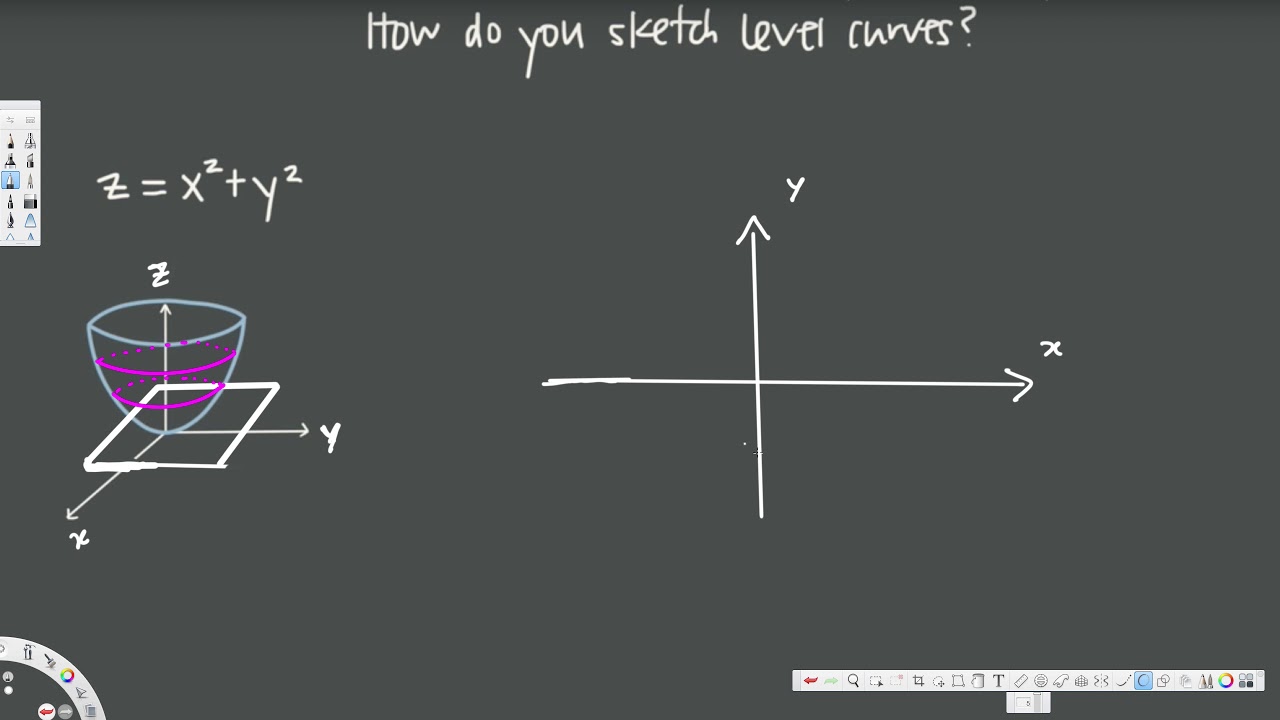



How Do You Sketch Level Curves Of Multivariable Functions Vector Calculus 1 Youtube




Describe The Level Curves Of The Function Z 8 2x 7y Chegg Com
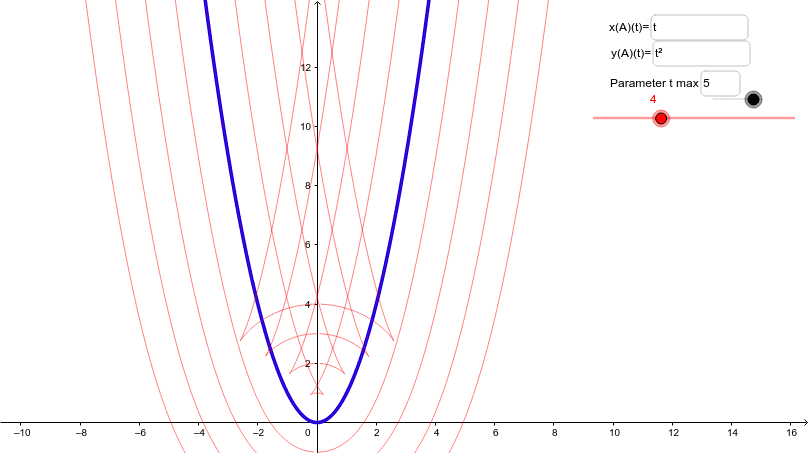



Level Curves Geogebra




The Graph Below Represents Some Level Curves Of A Chegg Com




If It Is Exact Find A Function F X Y Whose Differential Df X Y Gives The Differential Equation That Is Level Curves F X Y




Fx Cg50 Graphic Models School Lab Calculators Casio
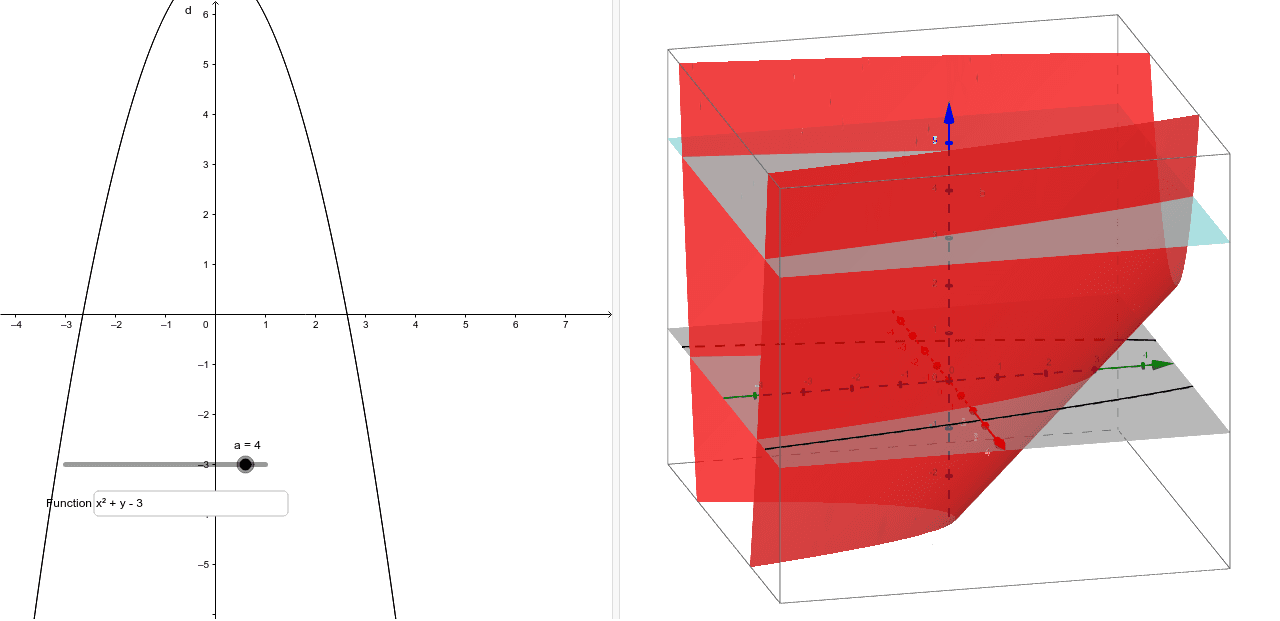



Visualizing Level Curves Geogebra



1
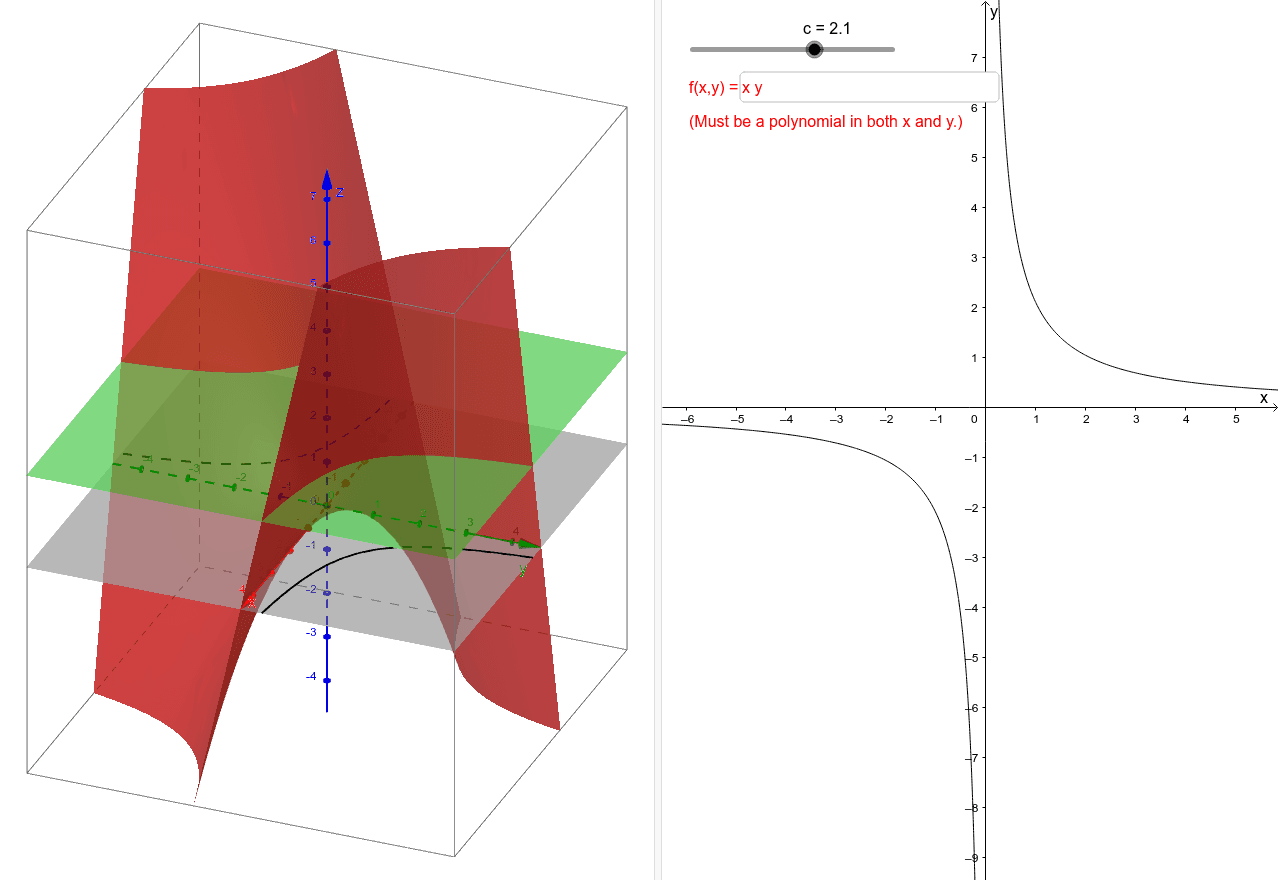



Level Curves Geogebra
:max_bytes(150000):strip_icc()/ScreenShot2020-02-11at7.47.59PM-eaa58305a83842519c6e1b32dcb2201c.png)



The 9 Best Graphing Calculators Of 21




Level Set Examples Math Insight



2




Level Surfaces
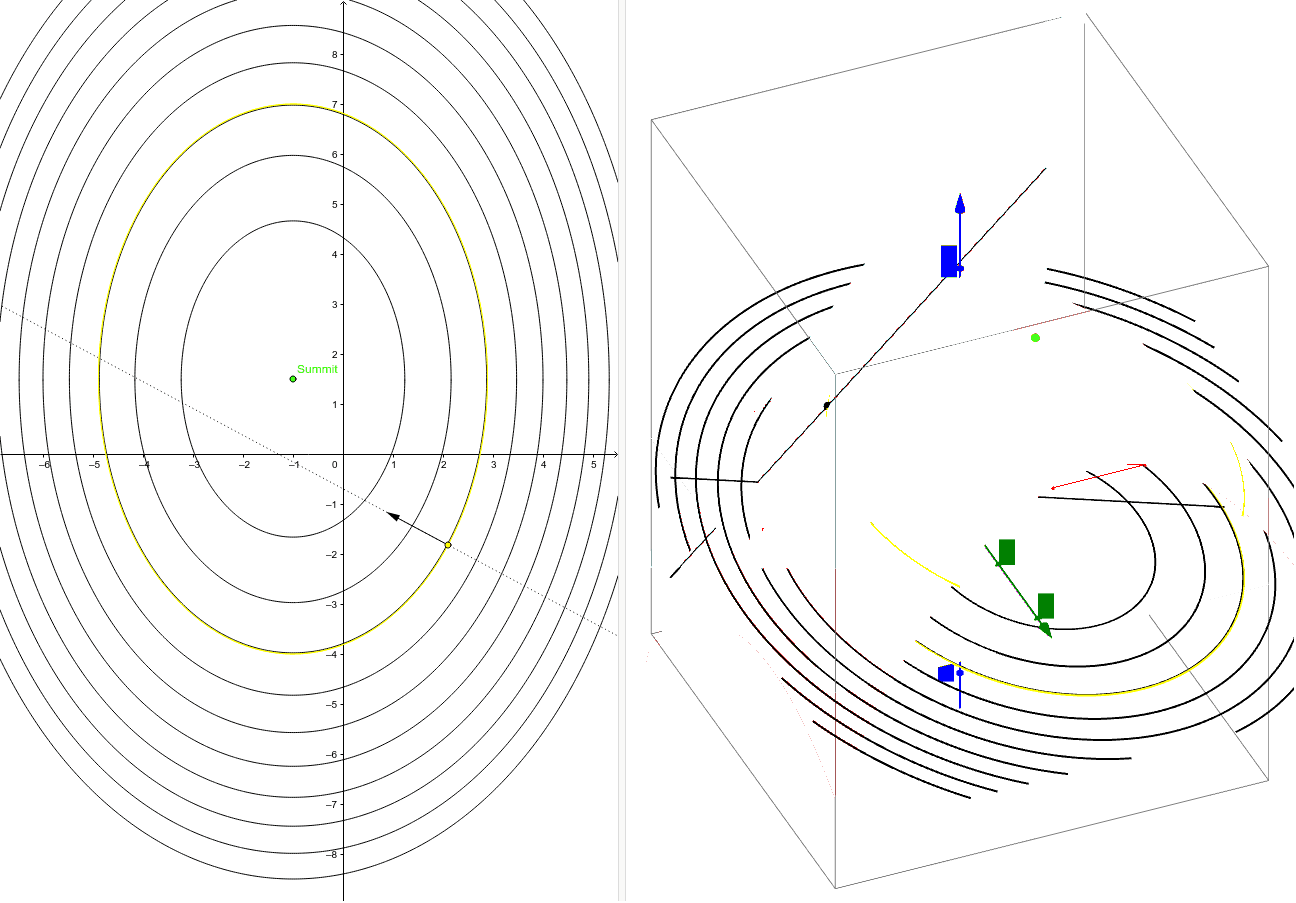



Gradient Vs Level Curves Geogebra




Fx Cg50 Graphic Models School Lab Calculators Casio
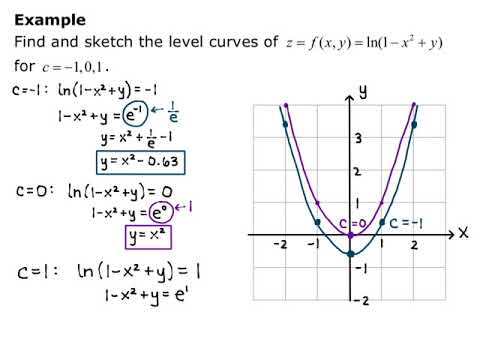



Section 13 1 Level Curves Youtube
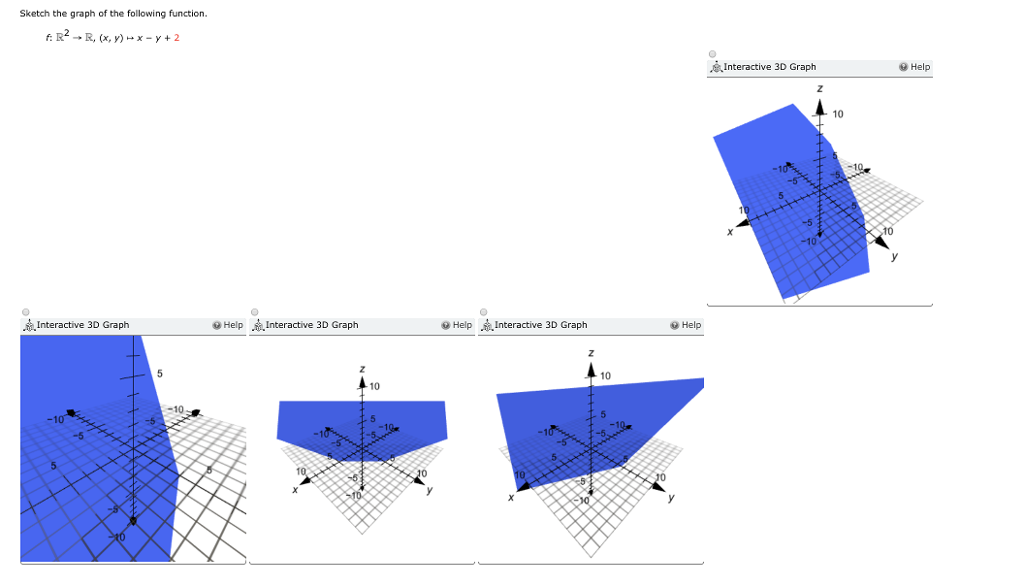



A Sketch The Level Curves Of The Following Chegg Com




Find The Domain And Range And Describe The Level The Chegg Com




M1c Exam1 Notes F14
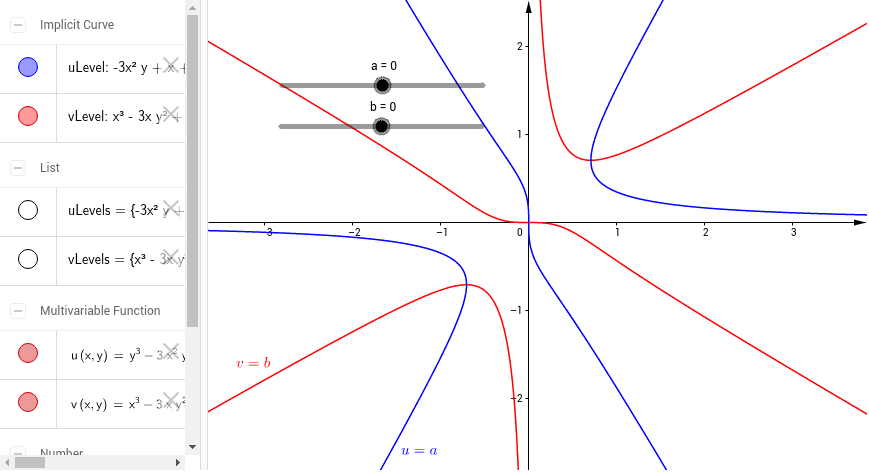



Level Curves Geogebra
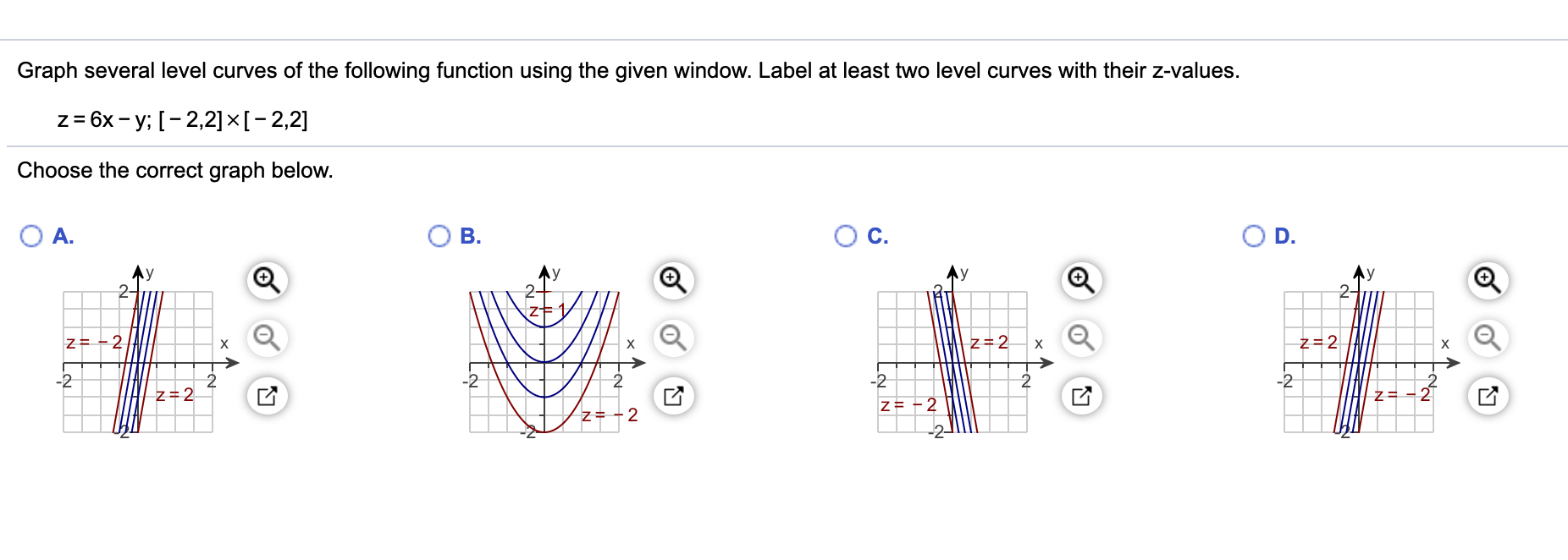



Graph Several Level Curves Of The Following Function Chegg Com
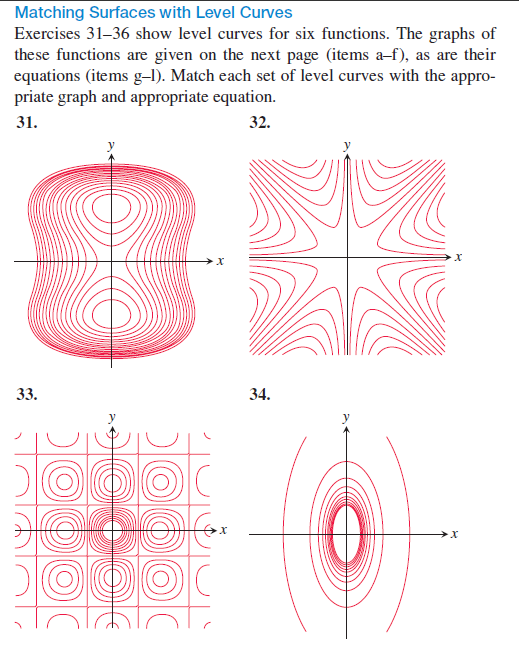



Matching Surfaces With Level Curves Exercises 31 36 Chegg Com




Area Under The Curve Calculator Find Area Under Curve



Level Curves



Desmos Accessibility
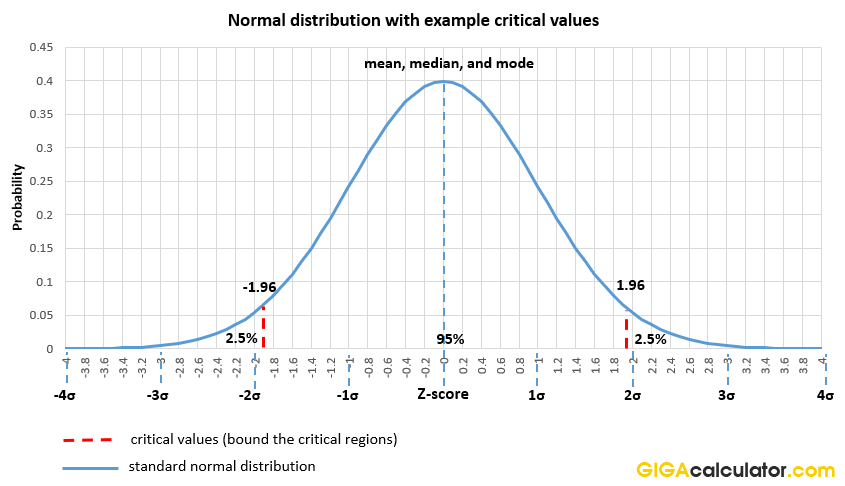



Normal Distribution Calculator With Formulas Definitions




Calculation Of The Temperature Field On The Strand Surface And Inside Download Scientific Diagram




Level Sets Ximera



0 件のコメント:
コメントを投稿